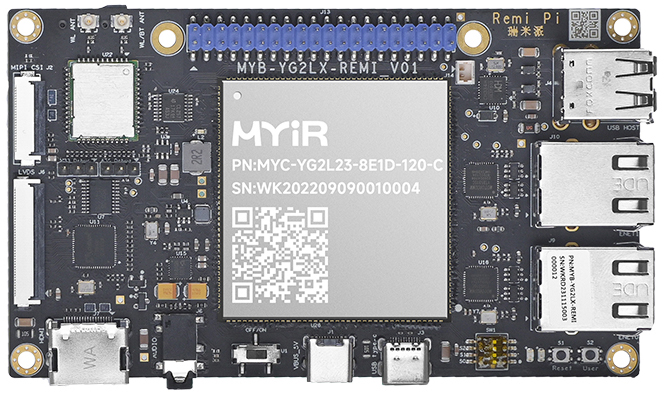
MYIR Remi Pi Features Renesas RZ/G2L SoC and Costs Just $55.00
MYIR Remi Pi is a Renesas RZ/G2L-based SBC, with dual Gigabit Ethernet ports, dual display support, and a MIPI-CSI camera interface. It also features 3D graphics functions powered by Arm Mali-G31. Additionally, it features HDMI, LVDS, and MIPI-CSI for seamless connectivity with various...
Continue Reading
The MINIX Z100-AERO – An Intel N100-Powered Mini PC with 2.5GbE and 1GbE Ethernet Support
The MINIX Z100-AERO is a compact mini PC powered by the Intel N100 CPU, designed to serve efficiently as a router when paired with software like Untangle or OPNsense. This device stands out due to its dual Ethernet ports: a 2.5GbE port managed by the TL8125BG-CG NIC and a 1GbE port...
Continue Reading
Hailo Closes New $120 Million Funding Round and Debuts Hailo-10, A New Powerful AI Accelerator Bringing Generative AI to Edge Devices
Hailo’s funding now exceeds $340 million as the company introduces its newest AI accelerator specifically designed to process LLMs at low power consumption for the personal computer and automotive industries, bringing generative AI to the edge. Hailo, the pioneering chipmaker of edge...
Continue Reading
Digi ConnectCore MP25 SoM Features STM32MP25 SoC with 1.35 TOPS NPU in a Tiny Form Factor
At Embedded World 2024, Digi International unveiled the Digi ConnectCore MP25, an ultra-compact System-on-Module (SoM) powered by the STMicroelectronics STM32MP25 SoC. This module is equipped with advanced connectivity features including 802.11ac Wi-Fi 5, Bluetooth 5.2, options for...
Continue Reading
Olimex VGA2HDMI is an Open Source VGA to HDMI Converter Board
Olimex has recently featured a new board named VGA2HDMI It is a VGA to HDMI converter board that can take in VGA signals and convert them into HDMI signals. The reason it's news is because one search will give you many HDMI to VGA converted and not the other way around. The company...
Continue Reading
Avnet Unveils MaaXBoard OSM93: A Powerhouse for Edge AI Development
Avnet introduces the MaaXBoard OSM93, a Raspberry Pi-style semi-single-board computer designed to cater to energy-efficient edge artificial intelligence (edge AI) tasks. The board leverages the NXP i.MX 93 system-on-chip (SoC) to power its capabilities, offering a versatile platform for...
Continue Reading
BeagleBoard’s New BeagleY-AI SBC Features Texas Instruments AM67A SoC with 4 TOPS Edge AI Accelerator
The BeagleBoard.org Foundation has recently released BeagleY-AI a Texas Instruments AM67A SoC powered SBC which promises open-source hardware in a standard form factor. The AM67A SoC features a quad-core Arm Cortex-A53 CPU, and dual DSPs with Matrix Multiply Accelerator, achieving a...
Continue Reading
MeLE PCG02 Pro Gets Intel Processor N100 Upgrade: Fanless Mini PC Stick Enhanced
The MeLE PCG02 Pro, known for its ultra-slim and fanless design, has received an upgrade with the latest Intel Processor N100 Alder Lake-N CPU. Initially introduced with an Intel Celeron J4125 (Gemini Lake Refresh) or Celeron N5105 (Jasper Lake) processor in 2022, the PC stick now...
Continue Reading