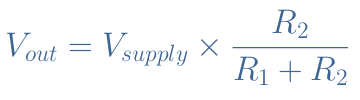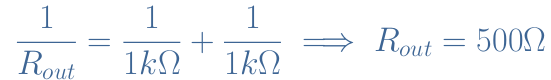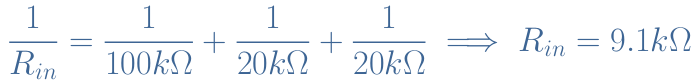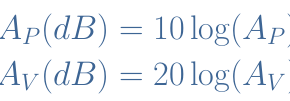Common Collector Amplifier

Presenting the Common Collector Amplifier

This article deals with another type of bipolar transistor architecture used to amplify signals that is commonly known as Common Collector Amplifier (CCA). The CCA can also sometimes be called emitter-follower amplifier and we will understand why later in this article.

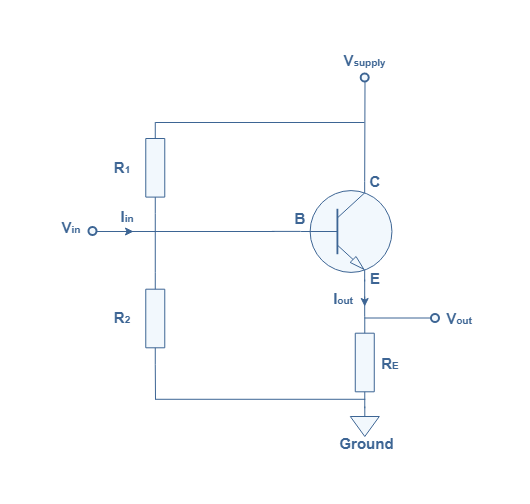
The first figure below is a simplified electric diagram with no particular biasing circuit presenting the CCA configuration :

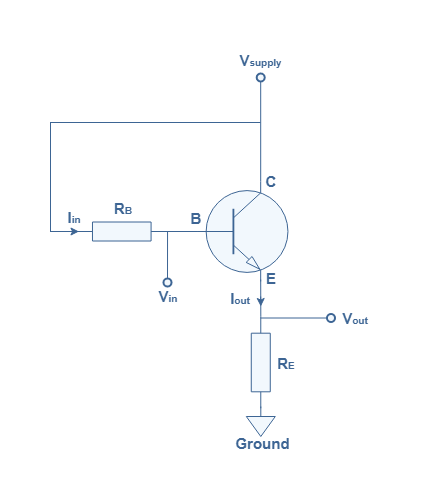
The main difference when comparing this architecture with the Common Emitter Amplifier (CEA) is that the output signals are taken on the emitter branch and the collector is always connected directly to the power supply, thus the name “Common Collector”.

It is shown further on that the voltage gain A_V=V_out/V_in is approximately equal to 1. Moreover, the phase remains the same during the amplification process, the input and output signals are therefore very similar, hence the name “emitter-follower”. On the other hand, we will see that the current gain A_C=I_out/I_in is high but has an upper limit.

Equivalent circuit

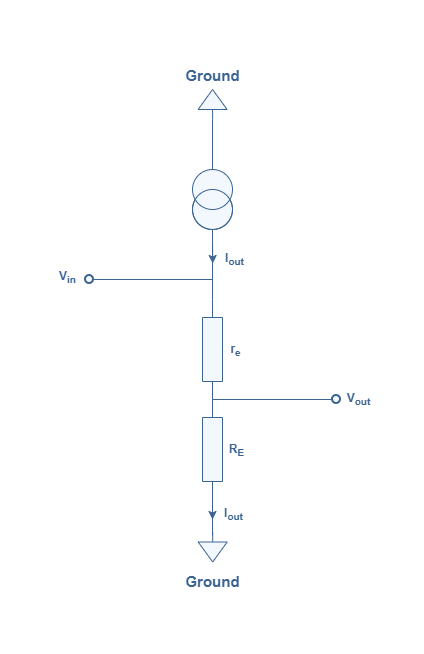
We can consider the bipolar transistor between the collector and emitter to be an ideal current source of amplification gain β where I_out=β.I_in. It also presents a small resistance given by r_e=25 mV/I_out known as “AC emitter resistance” or  “small diode emitter resistance” and represents the dynamic resistance for small AC signals of the p/n junction of the bipolar transistor.

We see in Figure 2 an equivalent circuit of the CCA configuration of Figure 1 considering the transistor such as described above.

Voltage gain

It is easy to understand that in the configuration presented in Figure 1, the voltage gain is approximately equal to 1. Let’s indeed consider the voltage loop between the base and emitter. It comes automatically that V_in=R_E.I_out=V_out and thus A_V=1.

From Figure 2 we can clearly express the input voltage to be V_in=(R_E+r_e).I_E and the output voltage to be V_out=R_E.I_E. When expressing the voltage gain A_V=V_out/V_in , the term I_E disappears and we get the exact expression of the gain A_V :

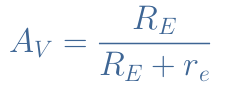
From this formula, it comes that A_V<1 but usually R_E>>r_e so the approximation A_V=1 is justified. Since the voltage gain is always smaller than 1, V_out<V_in : the CCA cannot provide any amplification for the voltage signal.

Biasing method

To provide better stability, the base of the bipolar transistor is biased with a voltage divider network such as shown in the following figure.

Since in a CCA configuration, V_in=V_out , the voltage divider network can be represented with a simpler equivalent circuit shown in Figure 4 :

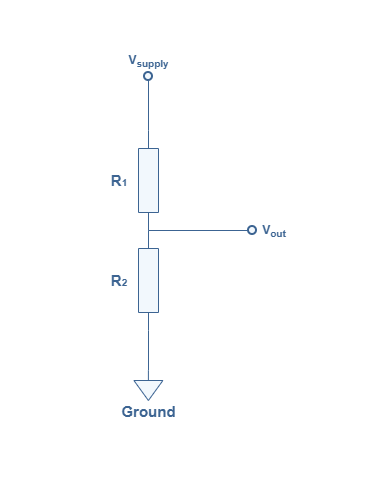
Using Kirchoff’s laws or Miller’s theorem in the circuit of Figure 4, it is easy to express the output voltage :

For a faithful amplification (no distortion or saturation), the output voltage should respect the condition V_supply=2.V_out. Thus, the bias resistances R₁ and R₂ should approximately be equal. However, to be more accurate, the threshold voltage between the base and emitter V_BE needs to be considered. For silicon-based bipolar transistors, the threshold voltage is a constant equal to V_BE=0.7 V.

The full expression of the output voltage is hence given by Equation 2 :

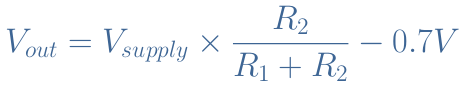
Input resistance

The CCA amplifier is characterized by a high input resistance. The expression of the base resistance R_B comes from Ohm’s law : R_B=V_in/I_in. We have previously seen that V_in=(R_E+r_e).I_out, thus :

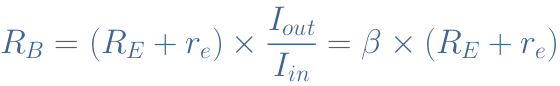
With the condition that R_E>>r_e the final expression of the base resistance can simply be written R_B=β×R_E. For this reason, the transistor’s current gain β is the most important factor to set the input resistance of a CCA configuration.

When considering a full CCA architecture with the biasing circuit, the total input resistance R_in satisfies the following formula :

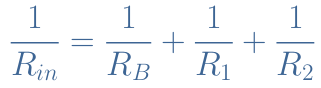
The input resistance of a CCA is always very high which is useful to avoid loading down previous circuits connected to it.

Output resistance

If we consider the circuit of Figure 1, the output resistance is given by the emitter resistance R_E which expression is R_E=R_B/β. However, the signal is always taken on a load resistance R_L in parallel with the emitter branch and in this case the output resistance satisfies :

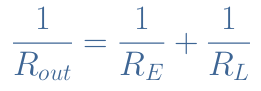
The output resistance on a CCA configuration is always very low and for this reason CCAs are used to drive low-resistance loads.

Current gain

Let’s consider a real CCA with a biasing circuit such as presented in Figure 3. The current gain A_C is expressed by the ratio A_C=I_out/I_in . The calculation of A_I depends on the values of the bias resistances :

• If the parallel resistance R₁//R₂ is much greater than the base resistance R_B, most of the current flows to the base and therefore I_in≅I_B so that A_C=β.
• If R₁//R₂ is lower or the same magnitude as R_B, the current gain needs to be determined by the formula A_C=I_out/I_in with I_in=V_in/R_in and R_in can be determined from Equation 4.

To sum up, if R₁//R₂>>β×R_E , A_C≅β. If not, A_C=I_out/I_in. The transistor gain β is thus the maximum current gain achievable by a CCA configuration.

Example : Voltage, Current and Power gains of Common Collector Amplifier

Having in mind the expressions and characteristics of the voltage gain, the input and output resistances, let’s consider the following circuit with a transistor gain of β=200 and determine the voltage, current and power gains.

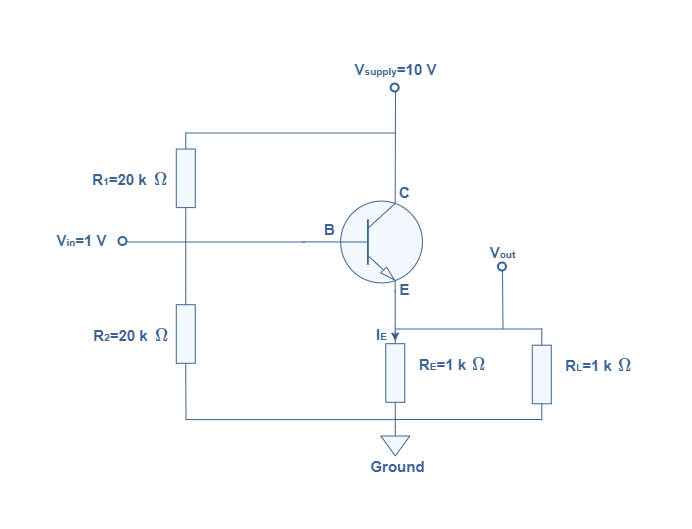
The output resistance is given by the emitter resistance R_E in parallel with the load resistance R_L :

The base resistance is given by R_B=β.R_out=200×500=100 kΩ. The input resistance is thus given by the base resistance R_B in parallel with the bias resistances R₁ and R₂ :

It can already be highlighted that R_in>>R_out such as mentioned previously. Let’s now calculate precisely the voltage gain A_V. It is first considered that A_V=1 so that Equation 2 is valid and therefore we can express the voltage drop across R_E such as :

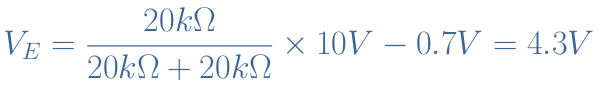
The current across the same resistance is thus given by I_E=4.3 V/1 kΩ=4.3 mA. The small AC resistance can then be determined by r_e=25 mV/4.3 mA=5.8 Ω. Since R_E=1 kΩ, we can confirm the hypothesis R_E>>r_e.

Finally, the voltage gain is expressed by A_V=500 Ω/505.8 Ω=0.989≅1.

In this example since R₁//R₂=10 kΩ<<R_B=100 kΩ the approximation A_C≅β is not valid and the current gain needs to be calculated with the formula A_C=I_out/I_in.To compute the current gain A_C, it is needed to determine the input and output currents I_in and I_out :

• The output current is simply I_out=V_out/R_out and since V_out≅V_in , I_out=1 V/500 Ω=2 mA.
• The input current is given by I_in=V_in/R_in=1 V/9.1 kΩ=110 μA.

Finally, the current gain is expressed by A_C=2 mA/110 μA=18.2.

The power gain is given by A_P=A_V×A_C=18. However, since R_E=R_L , the power given to the load is only half : A_P,load=9.

The Darlington pair

We have seen that the transistor’s current gain β is the factor limiting the total input resistance and the output current I_out=β.I_in. Indeed, if β increases, the base resistance R_B=β.R_E increases and therefore R_in increases as well.

A simple way to overcome that limitation without having to purchase an expensive specific high gain transistor is through the Darlington Pair (DP) presented below in Figure 6 :

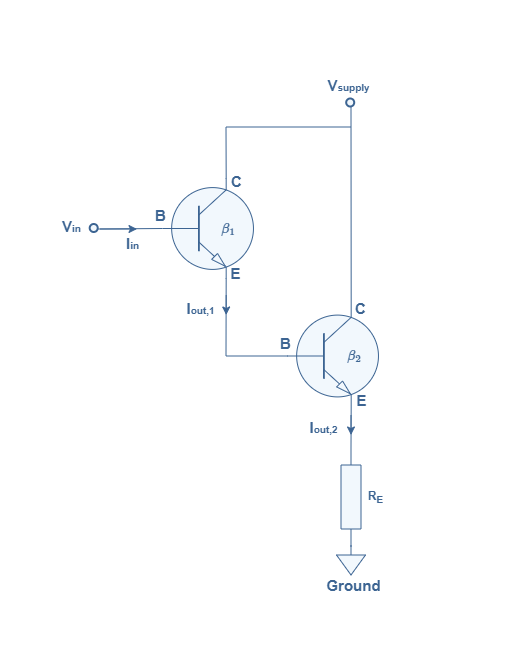
A DP consists in connecting together two bipolar transistor. The emitter of the first transistor is connected to the base of the second and both collectors are shorted to the power supply. We suppose the first transistor to have a gain β₁ and the second is β₂.

In this configuration, first of all, the input current is being amplified, the output of the first transistor is I_out,1=β₁.I_in. This same current I_out,1 becomes afterwards the input current of the second amplifier which is a CCA configuration. The final output current is I_out,2=β₂.I_out,1=β₁.β₂.I_in.

Finally, the total current gain of a DP is equal to Ω=β₁.β₂ which leads to a very high output current. Moreover, the base resistance can as well be expressed R_B=Ω.R_E which leads to a very high input impedance.

Conclusion

As a conclusion, we have seen that the Common Collector Amplifier does not amplify voltage signals since it’s voltage gain is strictly lower than 1 but usually can be approximated to 1, his nickname “emitter-follower” comes precisely from this behavior since the phase is also conserved. However, the current gain of a CCA is high with a upper limit equal to the transistor’s current gain β and depends on the values of the bias resistances. Moreover, we have seen that the input resistance is high and the output resistance is low. This characteristic makes the CCA configuration to be useful as a voltage buffer : the CCA can be interposed between a high and low impedance block to prevent any undesired loading. In the final section, we show an example of architecture called a Darlington pair that can overcome the limitation set by β for the input resistance and the output current.

In the next article, we present the last topology of the bipolar transistor : the Common Base Amplifier.

Please follow and like us: