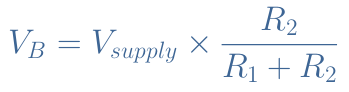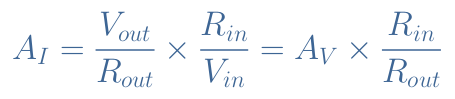Common Emitter Amplifier

Presenting the Common Emitter Amplifier

In the next three tutorials, including this one, we will present the three elementary topologies of bipolar transistors based amplifiers : the Common Emitter Amplifier, the Common Collector Amplifier and finally, the Common Base Amplifier.

We begin this series of tutorial by dealing with the most common type of amplifier found in an endless list of applications : the Common Emitter Amplifier that we will refer in the following as “CEA”.

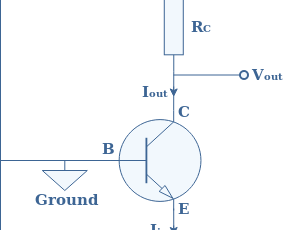
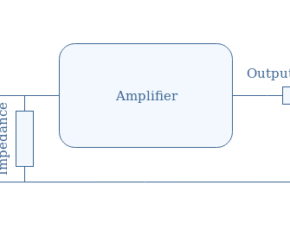
The first figure below presents the simplified electrical circuitry of a CEA configuration. The aim of Figure 1 is to purely show the general configuration of a CEA. However, some important elements of a real CEA architecture are missing and will be presented more in detail in the next section.

In this configuration, the input signal is delivered to the base branch, whereas the output is taken to the collector branch of the bipolar transistor. The name “Common Emitter” comes from the fact that the emitter branch is directly wired to the ground of the circuit.

Full CEA configuration

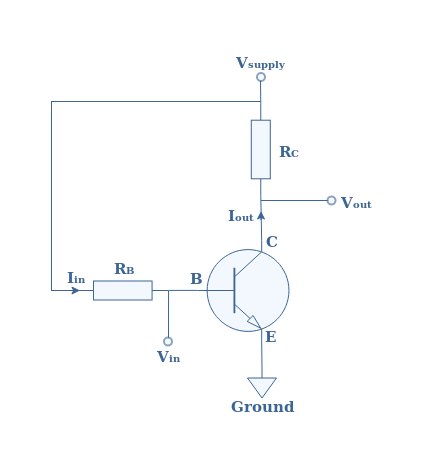
The simplified diagram given in Figure 1 does not include any biasing circuit, coupling and decoupling capacitors etc. A real circuit of a CEA configuration is given in Figure 2 :

First of all let’s deal with the added resistors:

• A resistance R_L is in parallel with the resistance R_C of the collector, it represents a load, that is to say the next stage of the circuit after the CEA : it can be an antenna, a speaker or simply another amplifier or stage of the electronic circuit.
• The resistance R_S represents the internal resistance of the sine source.
• The resistor R₁ and R₂ are in parallel with the base branch of the bipolar transistor and form what is commonly known as a voltage network divider. This voltage divider as shown in the tutorial “Biasing a Bipolar Transistor in Common Emitter Configuration” is the most suitable biasing method since it improves the stability of the amplifier.

Moreover, three capacitosr have been added :

• The capacitor C₁ and C₃ are commonly known as “coupling capacitors”. The coupling capacitance C₁ lets only the alternative current (AC) signal pass as an input of the CEA configuration while blocking the direct current (DC) to go from the supply to the source. The coupling capacitance C₃ does the same by blocking any DC component coming from or going to the load R_L. To summarize, C₁ and C₃ allow the AC signal to cross completely the CEA but blocks the DC signals to enter in the CEA.
• The emitter branch is wired to the ground through a “decoupling” or “derivation” capacitance C₂. It is shown later in the tutorial the importance of this capacitance to amplify the voltage signal.

With this configuration, the DC is restricted to bias the CEA and it sinks to the ground while the AC can cross the CEA from the input to the output. Since this circuit works with DC and AC signals, both need to be taken into consideration when analyzing the CEA configuration as it is done in the next two sections.

Equivalent circuit in DC

In DC, the coupling and decoupling capacitor act as an open circuit. Considering this fact, the equivalent circuit in DC of Figure 2 is presented in Figure 3 below :

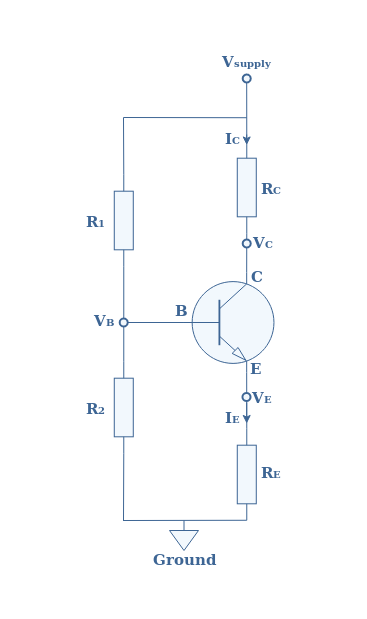
In this circuit, the base voltage V_B is given by the network divider formula :

The base resistance R_B is usually not considered in the calculation of V_B since it is in a parallel configuration with the bias resistances and its value is most of the time at least superior of one order of magnitude than R₂. However, for some configurations, this affirmation may not be valid or if one needs a high precision of the value of V_B, the full formula should include the base resistance R_B :

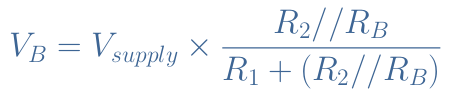
We can therefore express V_E=V_B-V_BE where V_BE=0.7 V is the threshold voltage of a silicon-based bipolar transistor.

Let’s suppose that the bipolar transistor current gain β is given by I_C=β×I_B with the collector current I_C and base current I_B, such as described in Figure 2. We have already mentioned just before that R_B>>R₂, moreover, since I_E≅I_C we can write from Figure 3 that R_B×I_B=R_E×I_C. When replacing I_C by β×I_B, the base current I_B simplifies itself and we get the expression of the base resistance :

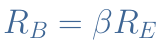
Equivalent circuit in AC

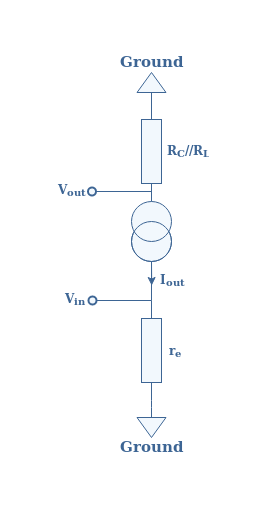
In AC, the coupling and decoupling capacitors are equivalent to a short circuit. Therefore, the emitter branch is shorted to the ground and the bias and collector are not included. Moreover, we introduce in the circuit a small diode emitter resistance r_e=25 mV/I_out that represents the dynamic resistance for small AC signals of the p/n junction of the bipolar transistor. When taking this into consideration, the equivalent circuit in AC of Figure 2 is given by Figure 4 below :

Input resistance

The total input resistance R_in of a CEA configuration is given by the parallel configuration of the bias and base resistances R₁//R₂//R_B :

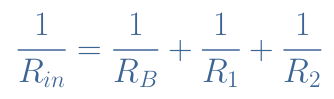
Output resistance

The total output resistance R_out of a CEA configuration is given by the parallel configuration of the collector and load resistances R_C//R_L :

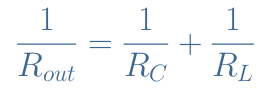
Voltage gain

The voltage gain of a CEA configuration is simply defined by A_V=V_out/V_in. When considering the circuit presented in Figure 4, we have V_out=R_out×I_out and V_in=r_e×I_out. The output current simplifies itself and the voltage gain is given by the ratio :

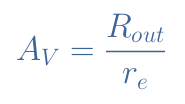
Equation 5 gives the expression of the voltage gain when the derivation capacitance behaves like a perfect short circuit, that is to say at high working frequencies.

Importance of the derivation capacitance

It is interesting to see the effect of the derivation capacitance C₂ presented in Figure 2. Indeed, if this capacitance is not used, the emitter branch is not shorted to the ground in Figure 4 and the total resistance in this branch is R_E+r_e instead of r_e. Therefore, the voltage gain becomes :

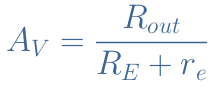
Usually the emitter resistance satisfies R_E>>r_e so that we can approximate the voltage gain by A_V=R_out/R_E. Since the emitter resistance is much greater than the small diode resistance, the voltage gain is very much decreased.

As an example, typical values are : R_C//R_L=1 kΩ, R_E=500 Ω and r_e=5 Ω.

• With no derivation capacitance, the voltage gain is A_V=1000/505=1.98
• With a derivation capacitance, the voltage gain becomes A_V=1000/5=200

The derivation capacitance in the emitter branch is therefore very important to amplify the voltage signal. Equation 6 gives the expression of the voltage gain when the derivation capacitance behaves as a perfect open circuit, that is to say at very low working frequencies or in DC mode.

Attenuation by the source

In Figure 4 we have not considered the source with its internal resistance R_S presented in Figure 2. In reality, the voltage gain is affected by a factor V_B/V_S that represents the dimming produced by the small internal resistance of the source. The attenuated voltage gain is A_V‘=A_V×(V_B/V_S) and this factor is given by :

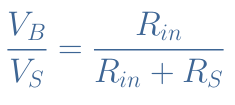
This factor is usually very close to 1 so often not considered to get an approximate value of the gain of a CEA configuration.

Current gain

The current gain is defined by A_I=I_out/I_in where I_in=V_in/R_in and I_out=V_out/R_out. It comes then :

The voltage gain A_V can be developed with the expression of Equation 5 which simplifies R_out and leaves :

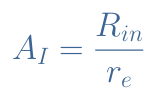
Since R_in>>r_e, the current gain of a CEA configuration is high.

Phase inversion

One very important characteristic of the CEA that we have yet not mentioned is that it inverts the phase of the output signals. Let’s consider for example a CEA with a voltage gain of 10 that has an input voltage of 2 V peak to peak and visualize both input and output voltages on the same figure :

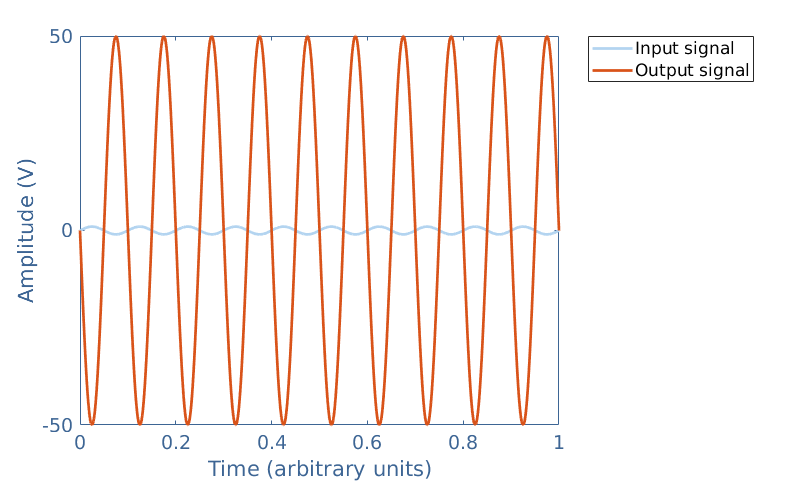
The phase inversion basically means that the maximum of the output voltage matches the minimum of the input voltage and the minimum of the output signal matches the maximum of the input signal.

Conclusion

In conclusion, we have seen how does a Common Emitter Amplifier (CEA) configuration behave. At first, a simplified circuit is presented to get introduced to the main aspects of this amplifier. We have seen afterwards the architecture of the full circuit of a CEA by understanding the role of bias and load resistor and coupling and decoupling capacitors. From analyzing the equivalent circuit in DC and AC modes, we have given the expressions of important parameters : the input and output impedance and the voltage and current gains. The CEA present high voltage and current gains that are enhanced by the presence of a derivation capacitance in the emitter branch, it also presents high input and output impedance, making it suitable as a universal amplifier for many applications. One other characteristic, specific only to CEAs is the phase inversion of 180 °=π rad between the input and output signals.

In the next tutorial we will analyze another type of amplifier that delivers the output from its emitter branch : the Common Collector Amplifier.

Please follow and like us: