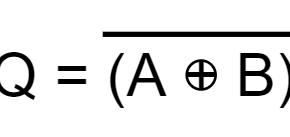Universal Logic Gates

Universal Logic Gates

The NAND and NOR logical gates are most commonly termed as Universal Logic Gates as they can be used to construct all other logical functions and Boolean expressions.

As it is learned from previous articles that AND, OR, and NOT are the most basic type of logic gates. They are the most basic building blocks of any digital or logic circuit. These logic gates can be used to construct any logical function or Boolean expression involving various theorems and laws of Boolean Algebra. The logic gates which can build any other logic function or Boolean expression are classified into “Set”. These AND, OR and NOT logic gates make a “Full Set” of Universal Logical Gates as each basic logic function is performed by an individual logic gate, individually.

On the other hand, AND & NOT logic gates can be used to produce OR logic. Likewise, OR & NOT logic can be used to produce AND logic. Thus, AND & NOT and OR & NOT gates can also be used to produce all three basic logical operations. They are termed as a “Complete Set” and this set using two logic gates (AND+NOT or OR+NOT) can produce all three basic logic operations.

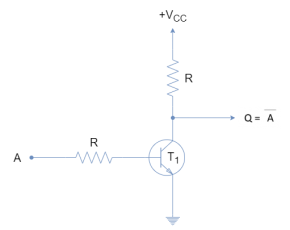
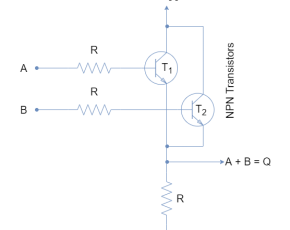
As described in previous articles, cascading of AND & NOT gates constructs a NAND logic gate. Whereas, as seen above, AND & NOT gates make a “Complete Set” to produce all three basic logic operations i.e. AND, OR, and NOT. So, ultimately, only the NAND logic gate (AND+NOT) can be used (in combinations) to produce other logic operations. Likewise, the combination of OR & NOT gates, the NOR logic gate can also be used to produce other logic operations. The NAND or NOR logic gates constitute the “Minimal Set” as by only using any of them all other logic functions or Boolean expressions can be constructed.

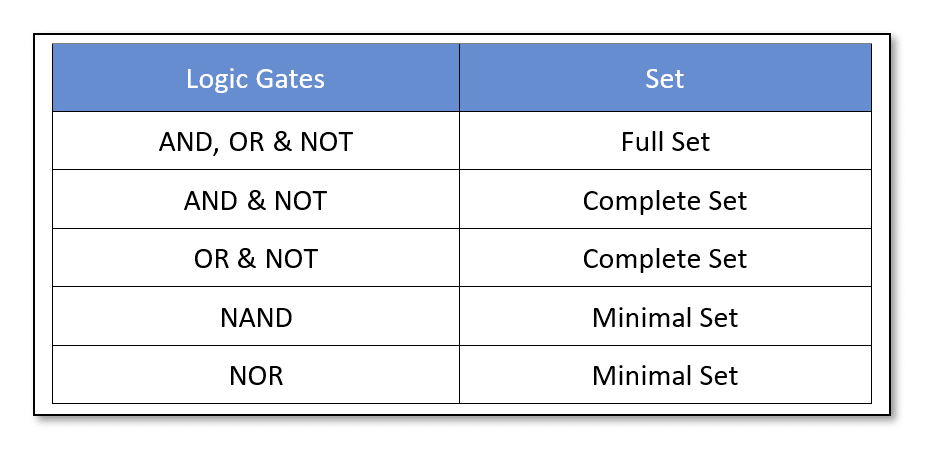
In the above table, five logic gate sets are listed and by using logic gates from each set complex combinational logic circuits can be constructed. Before proceeding further, let us recall the logical operations, switching characteristics and truth tables of three basic logic gates:

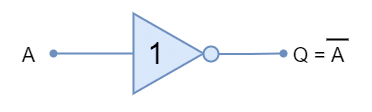
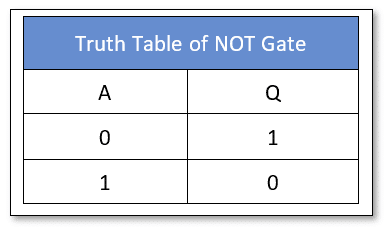
The Logic NOT Gate

The logic “NOT” gate, produces the inverse (NOT) of the input signal. It complements the input and produces it at the output. It does not perform any logical decision like AND & OR gates. It is denoted by a triangle having an “Inversion Bubble” at the output side. The “Inversion Bubble” represents an inversion, complement, or opposite of the incoming signal. It has a single input and single output. The cascading of another “NOT” gate will revert the signal to the original input. This double inversion constitutes a Digital Buffer that is used to amplify the input signal and/ or to isolate input and output circuits.

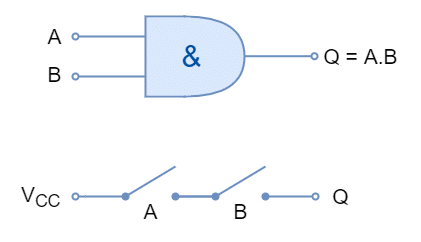
The Logic AND Gate

The logic “AND” gate performs multiplication on the digital inputs. The output of the logical “AND” gate represents the product (multiplication) of its digital inputs just like a mathematical multiplication. It is represented by a dot (.) between operands (inputs). It has two inputs and one output. The inputs of the “AND” gate can be extended by cascading the “AND” gates.

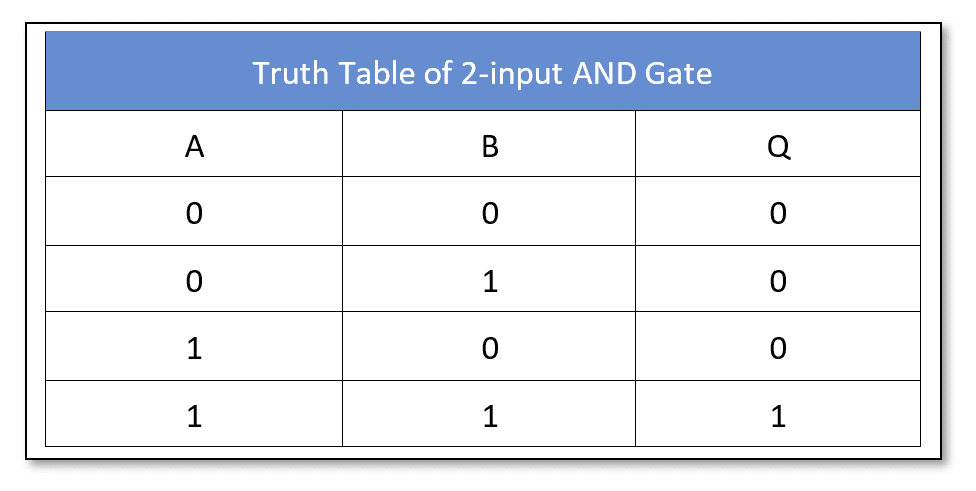
The Logical OR Gate

The Logical “OR” gate performs the addition of digital inputs. The output of the logical “OR” gate represents the summation (addition) of its inputs just lie a mathematical addition. It is represented by a plus (+) sign between the operands (inputs). It has two inputs and one output. The inputs of the “OR” gate can be extended by cascading the “OR” gates.

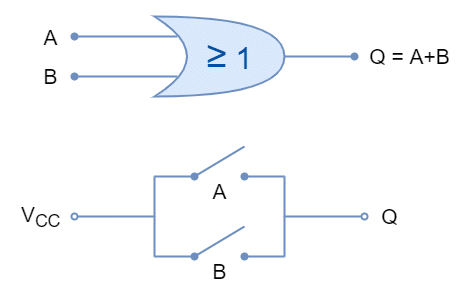
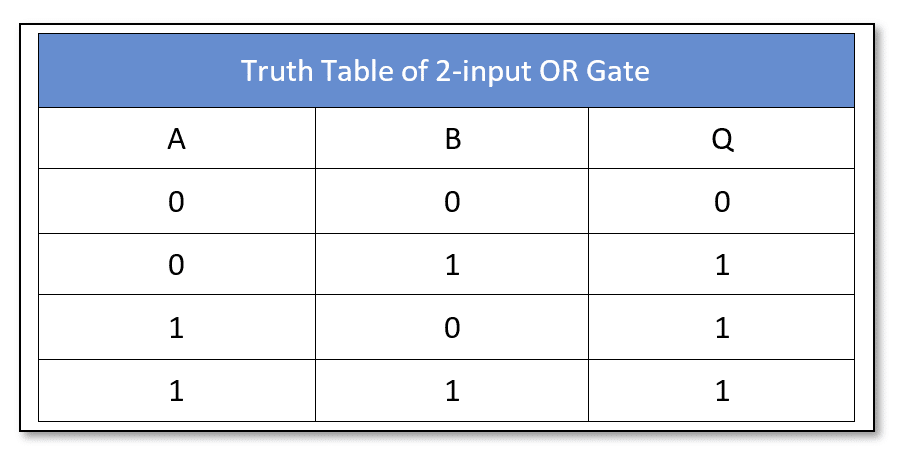
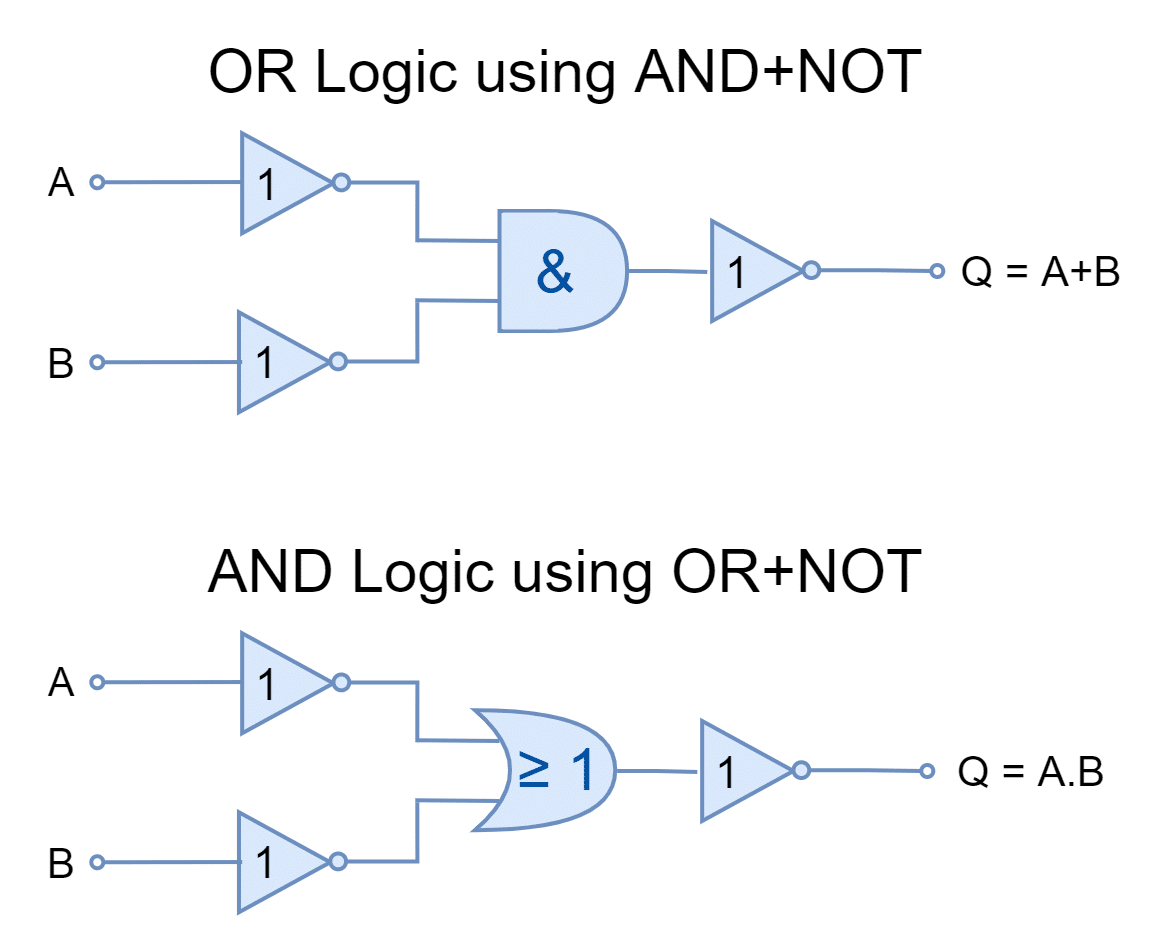
Now, the “Complete Sets” of AND & NOT and OR & NOT logic gates are used to construct basic logic gates.

Using AND & NOT Complete Set

In the following figure, the basic logic gates are constructed using only AND & NOT gates. The gates constructed are equivalent of AND/ NOT set equivalent.

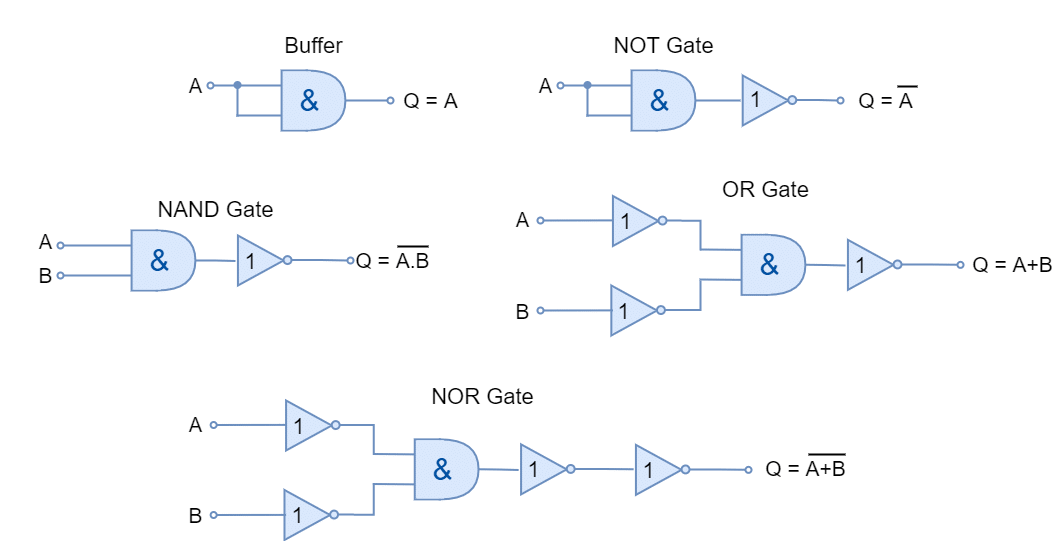
Using OR & NOT Complete Set

In the following figure, the basic logic gates are constructed using only OR & NOT gates. The gates constructed are equivalent of OR/ NOT set equivalent.

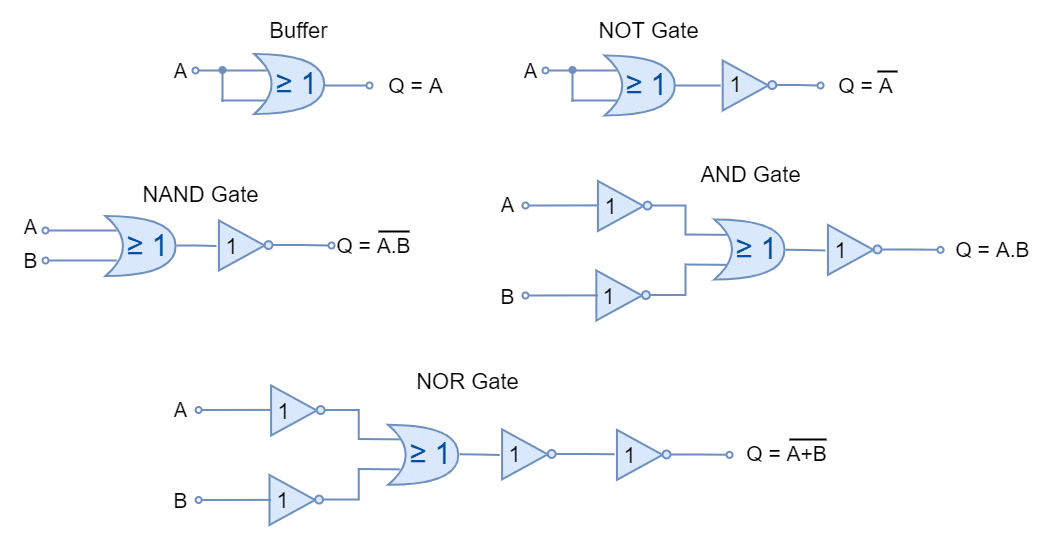
Using AND, OR, and NOT Full Set

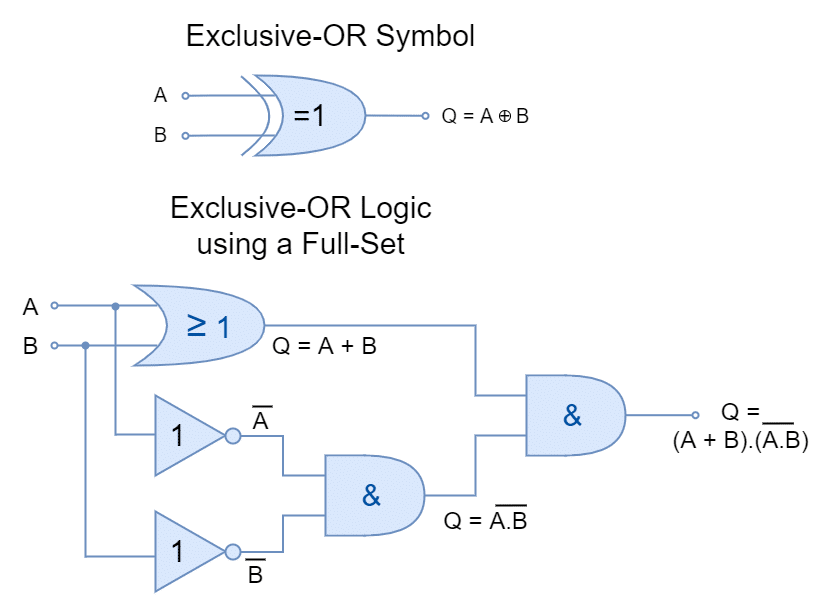
It is eminent from previous lectures that using AND, OR, and NOT (Full Set), any logic function and Boolean expression can be constructed. In the following figure, an exclusive-OR (XOR) logic gate is constructed using gates from Full Set.

Likewise, using a Full Set, an exclusive-NOR (XNOR) logic gate is constructed in the following figure.

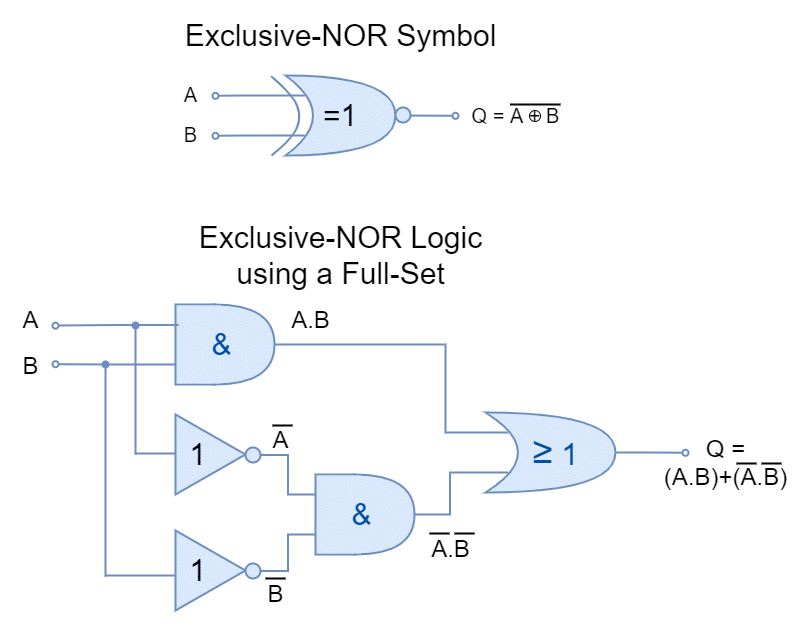
It is pertinent to mention here that the aforementioned Exclusive-OR and Exclusive-NOR gates are not classified as Universal Gates because they cannot produce other logic or Boolean functions.

Universal Logic Gates

The Minimal Sets of NAND and NOR gates are most commonly referred to as Universal Logic Gates. Using only NAND or NOR logic gate, any other logic function can be constructed. Using a single type of logic gate for the construction of logic function is preferable. The Full Set (AND, OR, and NOT) and Complete Sets (AND/NOT and OR/NOT) can also be used to construct logic functions but it contains different logic gates. It is not preferable to use different logic gates for the construction of logic as the same type of logic gates are usually manufactured in a single package and using different logic gates in a digital circuit would require different IC packages. Comparatively, using NAND or NOR only requires only a single IC package such as using 74LS00 (quad 2-input NAND TTL) or 74LS02 (quad 2-input NOR TTL) IC package a number of logic functions can be produced.

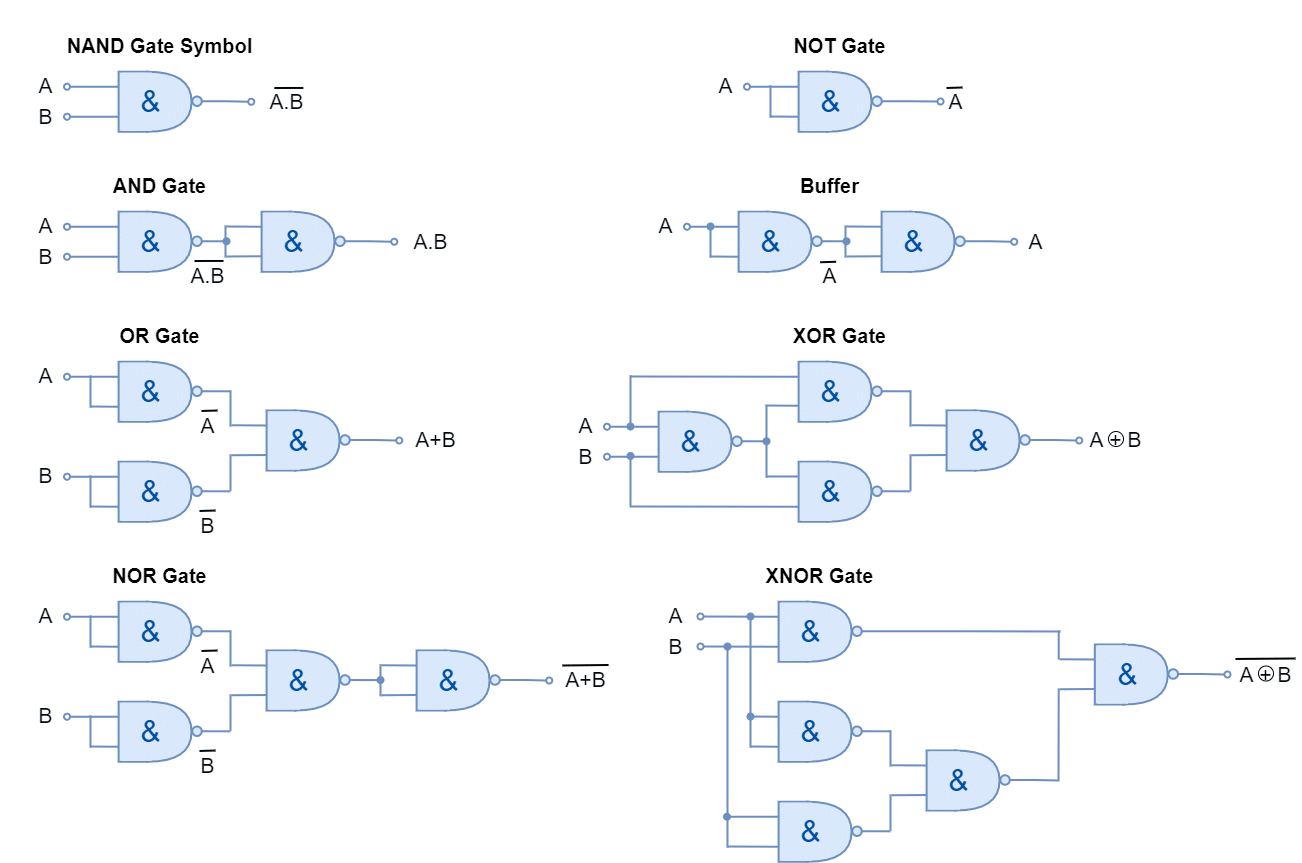
Using NAND Gates

In the following figure, other logic functions are constructed using only NAND gates. The commercially available 7400 TTL  (74LS00 or 74HC00) quad 2-input NAND IC package contains four individual NAND gates. The four NAND gates of the 74LS00 IC package are used to produce all other logic functions.

Using NOR Gates

In the following figure, other logic functions are constructed using only NOR gates. The commercially available 7402 TTL (74LS02 or 74HC02) quad 2-input NOR IC package contains four individual NOR gates. The four NOR gates of the 74LS02 IC package are used to produce all other logic functions.

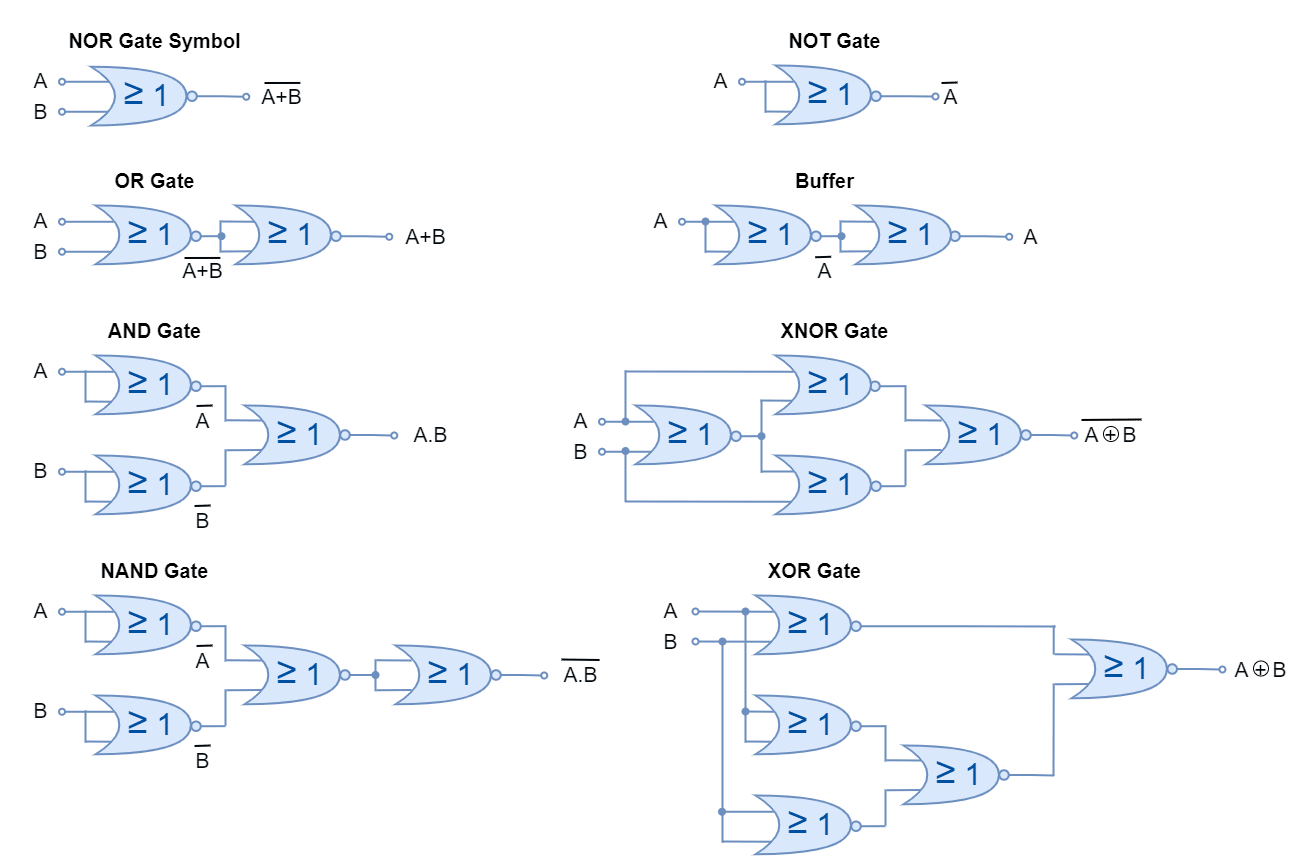
It is clear from the above figures that the construction of Exclusive-OR gate requires four (04) NAND or five (05) NOR gates. The Exclusive-OR (XOR) gate produced from NAND gates is more efficient compared to the one constructed from NOR gates.

Conclusion

• The Universal Logic Gates are the ones that can produce any other logic or Boolean expression.
• The AND, OR, and NOT are the basic gates and can produce any logic or Boolean expression. The logic gate(s) which can produce any other logic are grouped as a “Set”. These AND, OR, and NOT basic gates constitute a “Full Set”.
• The AND+NOT and OR+NOT gate sets can also be used to produce any other logic and these gate sets make a “Complete Set”.
• The NAND and NOR logic gates constitute a “Minimal Set”’ and are commonly termed as Universal Logic Gates. The NAND or NOR gate individually or in combination can produce any other logic function or Boolean expression.
• Commercially available Quad 2-input NAND (74LS00) and Quad 2-input NOR (74LS02) IC packages contain four individual gates and can produce all other logic functions.

Please follow and like us: